透过表象看本质！？之二数据拟合-白红宇

透过表象看本质！？之二数据拟合

阅读量：5950 次

发布时间：2019-06-19

本文共 4139 字，大约阅读时间需要 13 分钟。

假设对观测数据进行拟合，得到的拟合曲线为 $\hat y%$ 。将观测数据 ${x_i}%$ 代入 $\hat y%$ ，得到 $\hat y\left( {{x_i}} \right)%$ ，其和 ${y_i}%$ 的偏差定义为

${d_i} = g\left( {{y_i} - \hat y\left( {{x_i}} \right)} \right)%$ （1）

评价 $\hat y%$ 拟合结果好坏的函数称为指标函数

$I\left( {\hat y} \right) = h\left( {{d_1},{d_2}, \cdots ,{d_n}} \right)%$ （2）

拟合函数 $\hat y%$ 在观测数据上总的偏差越小，说明拟合的越好，因此 $I\left( {\hat y} \right)%$ 可以具体写成

$I\left( {\hat y} \right) = h\left( {{d_1},{d_2}, \cdots ,{d_n}} \right) = \sum\limits_{i = 1}^n {{\omega _i}{d_i}}%$ （3）

其中 $\sum\limits_{i = 1}^n {{\omega _i}} = 1%$ ， ${\omega _i}%$ 是加权系数，表示每个观测数据的重要程度。一般情况下，我们认为每个观测数据是等重要的。因此，上式可以简化为

$I\left( {\hat y} \right) = \sum\limits_{i = 1}^n {{d_i}}%$ （4）

其中偏差可以定义为

$g\left( \cdot \right) = {\left| \cdot \right|_p}%$ （5）

当p=0时， ${d_i} = g\left( {{y_i} - \hat y\left( {{x_i}} \right)} \right) = {\left| {{y_i} - \hat y\left( {{x_i}} \right)} \right|^0}%$

当p=1时， ${d_i} = g\left( {{y_i} - \hat y\left( {{x_i}} \right)} \right) = {\left| {{y_i} - \hat y\left( {{x_i}} \right)} \right|}%$

当p=2时， ${d_i} = g\left( {{y_i} - \hat y\left( {{x_i}} \right)} \right) = {\left| {{y_i} - \hat y\left( {{x_i}} \right)} \right|^2}%$

。。。

评价函数 $I\left( {\hat y} \right)%$ 一般写成p范数的p次方

$I\left( {\hat y} \right) = \sum\limits_{i = 1}^n {{d_i}} = \sum\limits_{i = 1}^n {g\left( {{y_i} - \hat y\left( {{x_i}} \right)} \right)} = \sum\limits_{i = 1}^n {{{\left| {{y_i} - \hat y\left( {{x_i}} \right)} \right|}_p}} = \left\| {y - \hat y\left( x \right)} \right\|_p^p%$ （6）

求最优拟合函数 $\hat y%$ 的过程是在 $\hat y%$ 和 $I\left( {\hat y} \right)%$ 构成的空间上寻优的过程

$\mathop {\min }\limits_{\hat y} I\left( {\hat y} \right) = \mathop {\min }\limits_{\hat y} \left\| {y - \hat y\left( x \right)} \right\|_p^p%$ （7）

对应的解是

$\hat y^*} = \mathop {\arg \min }\limits_{\hat y} I\left( {\hat y} \right) = \mathop {\arg \min }\limits_{\hat y} \left\| {y - \hat y\left( x \right)} \right\|_p^p%$ （8）

指标函数是一个以函数为自变量的函数。至此，这个问题是变分问题（至于说如何使用变分来求解，暂且压一压，以后再细说）。

假设拟合函数为 $\hat y = X\beta%$ 。 $Y=\begin{bmatrix}y_{1}\\ y_{2}\\ \vdots\\ y_{n}\end{bmatrix}%$ ， $X=\begin{bmatrix} 1 \, x_{1}\\ 1 \, x_{2}\\ \vdots \, \vdots\\ 1 \, x_{n} \end{bmatrix}%$ ， $\beta=\begin{bmatrix} \beta_{1}\\ \beta_{2}\\ \end{bmatrix}%$ 。

如何求出 $\beta%$ 呢？，从p=2开始推导。

$\min I\left( \beta \right) = \min \left\| {y - \hat y\left( x \right)} \right\|_2^2 = \min \left\| {Y - X\beta } \right\|_2^2%$

评价函数对 $\beta%$ 求导（因为在 $\beta%$ 的取值范围是连续的，且向量的 $\left\| \cdot \right\|_2^2%$ 是一个凸函数，至少是不凹的），

$\frac{d}{{d\beta }}I\left( \beta \right) = \frac{d}{{d\beta }}\left\| {Y - X\beta } \right\|_2^2 = - 2{\left( {Y - X\beta } \right)^T}X%$ （9）

$\frac{d}{{d{\beta ^T}}}\left( {\frac{d}{{d\beta }}I\left( \beta \right)} \right) = \frac{d}{{d{\beta ^T}}}\left( { - 2{{\left( {Y - X\beta } \right)}^T}X} \right) = 2{X^T}X%$ （10）

当 $\frac{d}{{d\beta }}I\left( \beta \right) = 0%$ 时， $\frac{d}{{d{\beta ^T}}}\left( {\frac{d}{{d\beta }}I\left( \beta \right)} \right) \ge 0%$ ，因此极值点为极小值点。

$\frac{d}{{d\beta }}I\left( \beta \right) = 0%$ 等价于

${\left( {Y - X\beta } \right)^T}X = 0%$ （11）

上式两边进行转置，得

${X^T}Y = {X^T}X\beta%$ （12）

X为列满秩矩阵， ${X^T}X%$ 的逆矩阵存在。因此

$\hat \beta = {\left( {{X^T}X} \right)^{ - 1}}{X^T}Y%$ （13）

$\hat Y = X\hat \beta = X{\left( {{X^T}X} \right)^{ - 1}}{X^T}Y%$ （14）

当p=0时， $\min I\left( \beta \right) = \min {\left\| {y - \hat y\left( x \right)} \right\|_0} = \min {\left\| {Y - X\beta } \right\|_0}%$ 。该式表示，拟合直线穿过观测数据点越多越好。该方法对数据的分布以及其中掺杂的噪声比较敏感，解不稳定。该方法可能不能拟合出真实数据的曲线，而是拟合了噪声数据。

当p=1时， $\min I\left( \beta \right) = \min {\left\| {y - \hat y\left( x \right)} \right\|_1} = \min {\left\| {Y - X\beta } \right\|_1}%$ 。评价函数导数不连续，求解不像二范数求解那么方便，因此很少使用，但在有些情况下，1范数拟合的曲线更好。

下面用一段代码，简单说明一下p范数对拟合结果的影响

lens=50;b=50; x=1:lens;y=2*x+b*randn(1,lens); x=[1 2 3 4 5];y=[1 2 2 3 5]; for k=1:200    for b=1:200        yk=(k-100)/10*x+(b-100)/10;        d=y-yk;        sign=ones(1,lens);        sign(find(abs(d)<0.5))=0;        err0(k,b)=sum(sign);        err1(k,b)=sum(abs(d));        err2(k,b)=sum(d.*d);    endendfigure(1)mesh(err0)figure(2)mesh(err1)figure(3)mesh(err2) figure(4)plot(x,y,'ro')hold on [a1 a2]=min(err0);[b1 b2]=min(a1);ka0=(a2(b2)-100)/10;ba0=(b2-100)/10;yk0=ka0*x+ba0;plot(x,yk0,'md')  [a1 a2]=min(err1);[b1 b2]=min(a1);ka1=(a2(b2)-100)/10;ba1=(b2-100)/10;yk1=ka1*x+ba1;plot(x,yk1,'g+')  [a1 a2]=min(err2);[b1 b2]=min(a1);ka2=(a2(b2)-100)/10;ba2=(b2-100)/10;yk2=ka2*x+ba2;plot(x,yk2,'bs')  e10=sum(abs(y-yk0))e11=sum(abs(y-yk1))e12=sum(abs(y-yk2)) e20=sum((y-yk0).*(y-yk0))e21=sum((y-yk1).*(y-yk1))e22=sum((y-yk2).*(y-yk2)) legend('data','L0','L1','L2')hold off

这段代码首先生成一组数据（x，y），然后分别使用0、1和2范数进行拟合求解。搜索范围k=[-10,10]，b=[-10,10]。在搜索空间中找到拟合误差最小的最小p乘解。

从评价函数的2范数出发， $\beta%$ 的解的形式中包含着复杂的矩阵运算关系，这其中应该蕴含着什么。让我们首先从一个简单的例子入手吧。

有a，b两个向量，b在a上的投影p可以写成投影长度x和a方向上单位向量的乘积

$p = \frac{a}{{\sqrt {{a^T}a} }}x = \frac{a}{{\sqrt {{a^T}a} }}\frac{{{a^T}b}}{{\sqrt {{a^T}a} }} = \frac{{a{a^T}}}{{{a^T}a}}b%$ （15）

往a方向上做投影的投影变换矩阵为

$P=\frac{{a{a^T}}}{{{a^T}a}}%$ （16）

$p=Pb%$ （17）

向量b到向量a的距离等于e=b-p的模，垂直方向上的投影矩阵为

${P_ \bot } = I - P%$ （18）

$e = b - p = b - Pb = \left( {I - P} \right)b = {P_ \bot }b%$ （19）

在数据拟合中，数据的个数远远多于未知数（待求解参数）的个数，因此这个方程不能得到精确解。我们需要找到距离Y最近的一个空间，将Y投影到该空间中。X的列向量构成的空间叫做列空间。该空间内的任意向量Xv都是X的列向量的线性组合得到，v就是组合系数。Y的近似解 $\hat Y%$ 形如

$\hat Y = X\hat \beta%$ （20）

近似解 $\hat Y%$ 与Y之间的向量为

$e = Y - \hat Y%$ （21）

该向量垂直于X的列空间中的任意向量Xv，有

${\left( {Xv} \right)^T}e = 0%$ （22）

${v^T}{X^T}\left( {Y - \hat Y} \right) = 0%$ （23）

因为v为任意向量，因此

${X^T}\left( {Y - \hat Y} \right) = 0%$ （24）

（20）式两边同时左乘矩阵X的转置，将（24）式代入得到

${X^T}Y = {X^T}X\hat \beta%$ （25）

解出

$\hat \beta = {\left( {{X^T}X} \right)^{ - 1}}{X^T}Y%$ （26）

近似解

$\hat Y = X\hat \beta = X{\left( {{X^T}X} \right)^{ - 1}}{X^T}Y%$ （27）

Y在投影变换矩阵 $P=X{\left({{X^T}X} \right)^{-1}}{X^T}%$ 的作用下，投影到X的列空间上，投影后得到的向量为 $\hat Y=PY%$ ，误差向量 $e = Y - \hat Y = \left( {I - P} \right)Y%$ ，误差的大小为 ${\left\| {Y - \hat Y} \right\|_p}%$ 。

投影矩阵从另外一个角度解释了最小二乘法，同时也是最小p（p>2）乘法的解释。我们发现，最小二乘法给出的解是近似解。误差的来源方方面面，比如系统偏差，观测误差，记录误差等等。这些因素之间是一个什么样的关系，线性的还是非线性的，一时半会儿说不清楚，我们偷个懒，将拟合问题重新形式化如下

$Y = X\hat \beta + \varepsilon%$ （28）

我们要求的问题等价于

$\hat \beta = \mathop {\arg \max }\limits_\beta p\left( {\left. Y \right|X,\beta } \right)%$ （29）

搞工程的搞来搞去不经意的发现，当随机不可知的因素很多，独立随机试验的次数很大时，由这些随机因素造成的随机误差服从高斯分布。学术界的人按耐不住了，不能让搞工程的压下去，整出了一个中心极限定理，各种分布都会渐进服从高斯分布。

我们俗气一把，还是从高斯分布入手，假设误差服从零均值高斯分布，即 $\varepsilon \sim N\left( {0,{\sigma ^2}} \right)%$ 。为什么是零均值，因为我们不想估计出个没用的有偏的分布出来。这种零均值误差还有个很带感的名字，白噪声。对其进行傅里叶变换后，各个频率都有响应，也就是说这种噪声是由不同频率的噪声合成的。我们常见的由各个频率合成的事物就是白色的光。所以，按照国际惯例，这种噪声叫做白噪声。

另外一个假设是独立同分布，也就是每次实验都是独立的，但是服从的分布相同。

$p\left( \varepsilon \right) = \frac{1}{{\sqrt {2\pi {\sigma ^2}} }}{e^{ - \frac{1}{2}{{\left( {\frac{\varepsilon }{\sigma }} \right)}^2}}}%$ （30）

$p\left( {\left. Y \right|X,\beta } \right) = \frac{1}{{\sqrt {2\pi {\sigma ^2}} }}{e^{ - \frac{1}{2}{{\left( {\frac{{Y - X\beta }}{\sigma }} \right)}^2}}}%$ （31）

令上式对 $\beta%$ 的导数为零，又见 ${X^T}Y = {X^T}X\hat \beta%$ 。也就是说，最小二乘法的概率解释是，拟合误差服从零均值高斯分布，拟合直线通过均值点。

假设噪声服从形如 $p\left( \varepsilon \right) = {e^{ - \left\| \varepsilon \right\|_p^p}}%$ ，那么其解对应的就是最小p范数解。这种分布貌似就是指数族分布，当p=1时叫做拉普拉斯分布，p=2时就是大名鼎鼎的高斯分布。

通过上面的分析，我们可以察觉到，噪声的模型影响了最终的拟合结果。如果噪声是形如1范数的，那么用2范数的最小二乘法拟合出来的直线就存在偏差。如果噪声中有粗大误差，那么如果不能事先去除，拟合的结果很有可能拟合了噪声而没能拟合真实数据。从这个角度看，其实我们能够解决的问题还比较有限，因为我们对于噪声的认识还不够。

从p范数的角度出发，均值是误差形如2范数的解，中位数是误差形如1范数的解，众数是误差形如0范数的解。猜想，p阶矩就是误差形如p范数的解。

到这里，我丧心病狂的把凸优化，线性代数和概率论貌似完美的在数据拟合的框架下联系在了一起。从其反方向看，这些理论本来就是为了解决数据拟合而被提出来的。只是数学教学时，人为的把本来应该在一起的拆开了。

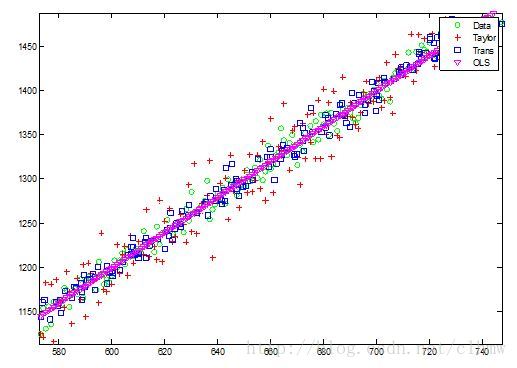
图中的数据在y=2x上加入了标准差为10的零均值高斯白噪声 $\varepsilon \sim N\left(0,100 \right)%$ 。使用上面推导的公式解出拟合曲线为

拟合误差的样本均值为0.abc%#%$^#e-13，样本标准差为9.44。同时，该拟合曲线通过样本的均值点。

a=4;b=10;lens=100; x=1:lens;y=zeros(1,lens);y=2*x+b*randn(1,lens); X=[x;y]'; Y0=zeros(lens,2);Y1=zeros(lens,2);Y2=zeros(lens,2);Y3=zeros(lens,2);pY=zeros(lens+10,2); A=zeros(lens,4);V=zeros(lens,4);D=zeros(lens,4);pY1=zeros(lens+10,2); figurefor i=1:lens    Y0(i,:)=X(i,:);           if i>3 && a>=4       Y3(i,:)=Y0(i,:)-3*Y0(i-1,:)+3*Y0(i-2,:)-Y0(i-3,:);    end    if i>2 && a>=3        Y2(i,:)=Y0(i,:)-2*Y0(i-1,:)+Y0(i-2,:);    end    if i>1 && a>=2        Y1(i,:)=Y0(i,:)-Y0(i-1,:);    end       pY(i+1,:)=Y0(i,:)+Y1(i,:)+0.5*Y2(i,:)+1/6*Y3(i,:);       if i

上面的代码中pY是基于泰勒级数展开的近似估计，pY1是基于局部最小二乘估计，pY2是全局最小二乘估计。

说了这么多，我们原地踏步在一阶线性估计上，高阶怎么求解。改改X和 $\beta%$ 就可以了。求解方法还是原来的配方，还是原来的味道。这里就不在多啰嗦了。

$X=\begin{bmatrix} 1&{x_1^1}& \cdots &{x_1^m}\\ 1&{x_2^1}& \cdots &{x_2^m}\\ \vdots & \vdots & \ddots & \vdots \\ 1&{x_n^1}& \cdots &{x_n^m} \end{bmatrix}%$ （32）

$\beta=\begin{bmatrix} {\beta_0}\\ {\beta_1}\\ \vdots\\ {\beta_m} \end{bmatrix}%$ （33）

给大家再拜上一记大杀器

$X=\begin{bmatrix} {h_0}\left( 1 \right)&{h_1}\left( {{x_1}} \right)& \cdots &{h_m}\left( {{x_1}} \right)\\ {h_0}\left( 1 \right)&{h_1}\left( {{x_2}} \right)& \cdots &{h_m}\left( {{x_2}} \right)\\ \vdots & \vdots & \ddots & \vdots \\ {h_0}\left( 1 \right)&{h_1}\left( {{x_n}} \right)& \cdots &{h_m}\left( {{x_n}} \right) \end{bmatrix}%$ （34）

小伙伴们不要害怕，看 $h\left( \cdot \right)%$ 一副卖萌的样子就知道这货是传说中的核函数。加权函数一块来的时候，更加凶残的公式也就来了

$\hat \beta = {\left( {{X^T}WX} \right)^{ - 1}}{X^T}WY%$ （35）

从数据出发，我们总能对它们进行合适的解释，发现合适的模型，拟合出合适的曲线，并给出这种解释的好坏程度。到目前为止，我们对于数据拟合能够给出的最简洁的表达是

${\hat y^*} = \mathop {\arg \min }\limits_{\hat y} I\left( {\hat y} \right) = \mathop {\arg \min }\limits_{\hat y} \sum\limits_{i = 1}^n {{\omega _i}\left\| {{y_i} - {x_i}\beta } \right\|_p^p}%$ （36）

貌似我们可以满足的洗洗睡了，但是一个关键的问题是X的具体形式能不能由数据自己说出来，也就是说从无到有可不可能。此外，还有两个问题没有解决，如何在保证上式成立的同时将参数的空间最小化，也就说能够用线性拟合的不用二阶多项式拟合。第二个问题就是迭代拟合。现实情况中，我们接收到的数据往往是以时间序列的形式呈现的，那t时刻和t-1时刻的模型出现不一致时，怎么处理。

未完待续

你可能感兴趣的文章